An Introduction to Cryptography

IDPro Body of Knowledgeの翻訳メモです。

元記事：https://bok.idpro.org/article/id/102/

IDPro Body of Knowledgeの翻訳メモのトップページ

Abstract

A non-technical introduction to cryptography, the foundation of security and privacy on the Internet.

As an IAM practitioner, you understand the central role digital identity plays in information technology and security. The confidentiality, integrity, and availability of digital identity services depend on reliable, trustworthy cryptographic systems. Understanding basic cryptography is the first step to understanding what makes a trustworthy cryptosystem.

Keywords: cryptography, public key cryptography, asymmetric key cryptography, symmetric key cryptography

概要

インターネットにおいてセキュリティとプライバシーの基盤である暗号学についての技術用語を使っていない入門記事です。

IAM実務者であれば、情報テクノロジーおよびセキュリティにおいてデジタルアイデンティティが中心的な役割を果たしていることを理解しているでしょう。デジタルアイデンティティサービスの機密性、完全性および可用性は、頼りになり、信頼できる暗号システムに依存しています。基礎的な暗号学を理解することは、信頼できる暗号システムを構築するものを理解する最初の一歩となります。

Keywords: 暗号学, 公開鍵暗号方式, 非対称鍵暗号方式, 共通鍵暗号方式

An Introduction to Cryptography

By Mark Drummond (Empire Life)

© 2024 IDPro, Mark Drummond

To comment on this article, please visit our GitHub repository and submit an issue .

Introduction

Cryptography is the science and art of secret writing—keeping information secret. (Garfinkel 1996)

For almost as long as we have been writing, we have tried to write in secret. The use of ciphers to make writing unintelligible to all but an intended recipient is at least as old as ancient Mesopotamia.

In the year 1567, Mary, Queen of Scots , was executed for her involvement in a plot to assassinate the then Queen of England, Elizabeth I. A cabal of conspirators planned to overthrow Elizabeth to install Mary on the Throne of England. Mary’s hand in the affair was proven using letters between Mary and the cabal. These letters were written in cipher, rendered unintelligible to the casual observer.

Queen Elizabeth’s spymaster, Sir Francis Walsingham, had been intercepting and making copies of Mary’s letters. He enlisted the help of Thomas Phelippes , a linguist and expert in ciphers, to decipher Mary’s letters. Phelippes was successful, and the content of the letters was revealed, making clear Mary’s involvement, thus giving Elizabeth the evidence she needed to have Mary put to death.

In the 21st century, secret communications are as important as ever, but there are additional protections we want to apply to our messages. The study of techniques for protecting communications is referred to as Cryptography.

Security practitioners use cryptographic systems to meet four fundamental goals: confidentiality, integrity, authentication, and non-repudiation. (Chapple 2021)

Cryptography has four main goals:

• Confidentiality (privacy, secrecy): keeping data secret from all but those authorized to see the data.

• Integrity: preventing and detecting the unauthorized—intentional or otherwise—modification of data.

• Authentication: positively identifying the parties to a communication and the source of data.

• Non-repudiation: methods preventing someone from denying an action they took or a decision they made.

導入

暗号学は、秘密を秘密のまま書くための科学であり、芸術です。（Garfinkel 1996）

私たちが何かを書ようになってからほとんどの場合、秘密裏に書こうとしてきました。意図した受信者を除いた全ての人に理解できないように書くための暗号の利用は少なくとも古代メソポタミア文明で確認されています。

1567年、スコットランド女王Maryは、イングランド女王Elizabeth Iの暗殺計画への関与によって処刑されました。イングランドの王位にMaryを即位させるため、Elizabethを打倒することを陰謀団は計画していました。この件へのMaryの関与は、Maryと陰謀団との間の手紙によって証明されました。これらの手紙は暗号によって書かれ、傍目には理解できませんでした。

Elizabeth女王のスパイマスターであったSir Francis Walsinghamは、Maryの手紙を傍受し、コピーを作成しました。彼はMaryの手紙を解読するため、言語学者であり、暗号の専門家であるThomas Phelippesの助けを借りました。Phelippesは成功し、手紙の内容が暴かれ、Maryの関与が明らかとなり、ElizabethにMaryを処刑するために必要な証拠を献上しました。

21正規において、秘密通信が重要であることは同じですが、メッセージに適用したい追加の保護があります。通信の保護する技術の学問は暗号学と呼ばれます。

セキュリティの専門家は、4つの基本的な目的のために暗号システムを利用します：機密性、完全性、認証そして否認防止（Chapple 2021）

暗号には主たる4つの目的があります：

• 機密性（プライバシー、秘密性）：データを閲覧することを認可された者を除き、データを秘密にすること。

• 完全性：データの認可されていない意図的もしくはその他の改変を防止し、検知すること。

• 認証：通信の当事者とデータのソースを積極的に特定すること。

• 否認防止：ある人がおこなったアクションまたはおこなった決定を否定することを防止する方法。

Terminology

I will follow the model of Singh’s The Code Book (Singh 2000) in using more approachable but arguably less accurate or consistent terminology and definitions. Terms such as encrypt and encipher are treated as synonyms. Readers should bear in mind that the technical literature on cryptography may use slightly different definitions.

Term	Synonyms	Definition
Asymmetric Key Cryptography	Public Key Cryptography	A cryptosystem in which a pair of keys is used to encrypt and decrypt data. The pair of keys has the unusual property that data encrypted with one can be decrypted only with the other.
Cipher	Encryption Algorithm	A method for transforming plaintext into ciphertext.
Ciphertext	—	Data that has been encrypted.
Cryptanalysis	—	The study of deciphering secret writing. Code breaking.
Cryptography	—	The study of secret writing. Code making.
Cryptology	—	The field of research encompassing both cryptography and cryptanalysis.
Cryptosystem	—	The collection of technologies providing cryptographic functions such as encrypting and decrypting data.
Decrypt	Decipher	To transform ciphertext into plaintext, rendering the data intelligible.
Encrypt	Encipher	To transform plaintext into ciphertext, rendering the data unintelligible.
Key	Secret, secret key, encryption key	Unique input to a cryptosystem that adds randomness to the encryption process. The security of a cryptosystem is predicated on the secrecy of the key.
Session Key	—	A temporary key used to encrypt data communications during a relatively short-lived session. At the end of the session, further communication requires the use of a new session key.
Plaintext	Cleartext	Data that has not been encrypted.
Symmetric Key Cryptography	Private Key Cryptography	A cryptosystem in which a single key is used to both encrypt and decrypt data.

用語解説

Singh氏の The Code Book （Singh 2000）のモデルに従い、より親しみやすく、正確性や一貫性にかける用語や定義を用います。encryptとencipherのような単語は同義語として扱います。読者は、暗号学における専門文献では若干異なる定義が用いられることがあることに注意してください。

用語	同義語	定義
非対称鍵暗号方式	公開鍵暗号方式	データの暗号化と復号のために一対のカギを使った暗号システム。一対の鍵は、一方で暗号化したデータはもう一方でのみ複合できるという性質を通常は有しています。
暗号（Cipher）	Encryption Algorithm	平文を暗号文に変換する方法。
暗号文（Ciphertext）	—	暗号化されたデータ。
暗号解析（Cryptanalysis）	—	秘密文を復号する研究。暗号解読。
暗号学（Cryptography）	—	秘密文の研究。暗号作成。
暗号理論（Cryptology）	—	暗号学と暗号解読の両方を含む研究分野。
暗号システム（Cryptosystem）	—	データの暗号化と復号のような暗号機能を提供する技術の集合。
復号（Decrypt）	Decipher	データの意味がわかるように、暗号文を平文に変換すること。
暗号化（Encrypt）	Encipher	データの意味がわからないように、平文を暗号文に変換すること。
鍵（Key）	Secret, secret key, encryption key	暗号化処理にランダム性を注入する、暗号システムへのユニークな入力。暗号システムのセキュリティは、鍵の秘密性によって決まります。
セッションキー（Session Key）	—	比較的短時間のセッションの間のデータ通信を暗号化するために利用される一時的な鍵。セッションの終わると、さらなる通信には新しいセッションキーの利用が必要です。
平文（Plaintext）	Cleartext	暗号化されていないデータ。
共通鍵暗号方式	秘密鍵暗号方式	A cryptosystem in which a single key is used to both encrypt and decrypt data.

Ciphers and Keys

… the secrecy of messages must depend upon a changeable key added to a sound basic cipher—Gaines (Gaines 2014) ¹

All modern cryptosystems rely on a “key”, analogous to a password ² . The key adds randomness to the encryption process, such that knowing the cipher alone is insufficient to decrypt the message. You can use new or additional keys as needed: a new key for every person you need to communicate with or a new key if you suspect an existing key has been compromised. Using a key-based system means your cipher can be made public, allowing experts to analyze it for flaws. It also means anyone can benefit from using your cipher to protect their data.

暗号と鍵

… メッセージの秘密性は、堅固で基本的な暗号に加える変更可能な鍵に依存しなくてはならない Gaines (Gaines 2014) ¹

全ての現代暗号システムは、パスワード ² に似た「鍵」に依存しています。この鍵は、暗号化処理にランダム性を加え、暗号を知っているだけではメッセージの復号に不十分であるようにします。必要であれば、新しいもしくは追加の鍵を使うことができます：通信をおこなう必要があるすべての人のための新しい鍵、もしくは既存の鍵が侵害されたと疑った場合の新しい鍵。鍵ベースのシステムを利用することは、専門家がその暗号の欠陥を解析できるように、暗号を公開することを意味します。また、データを保護するためにあなたの暗号を利用することで誰もが利益を得ることができることを意味します。

Symmetric Key Cryptography

Encryption is the process by which a message (called plaintext) is transformed into another message (called ciphertext) using a mathematical function and a special encryption password, called the key. (Garfinkel)

Symmetric key cryptography uses a single key to encrypt and decrypt messages:

共通鍵暗号方式

暗号化とは、メッセージ（平文と呼ばれる）を別のメッセージ（暗号文と呼ばれる）に、数学的な手法と鍵と呼ばれる特別な暗号パスワードを利用して変換する処理です。（Garfinkel）

共通鍵暗号方式は、メッセージの暗号化と復号のために単一の鍵を使います：

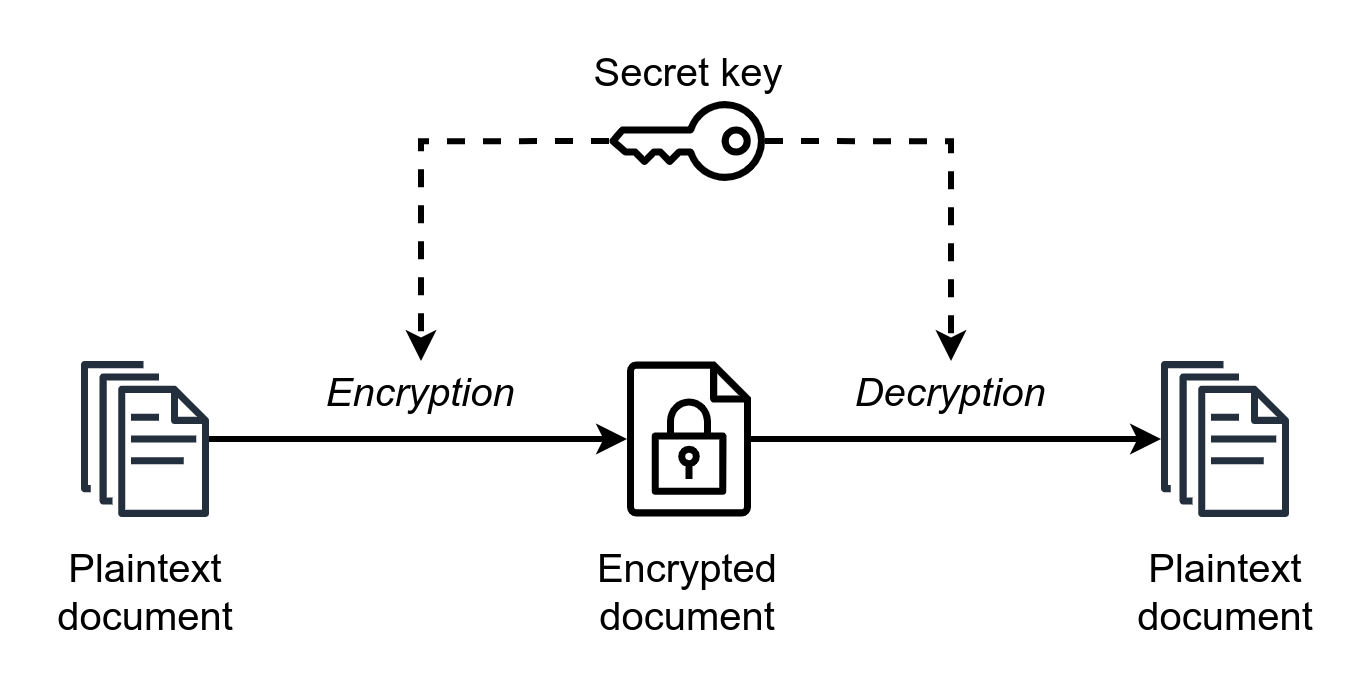
Figure 1: Symmetric Key Cryptography

MarcT0K (icons by JGraph), CC BY-SA 4.0 , via Wikimedia Commons

Consider the following use case:

1. Alice ³ wants to send a secret message to Bob. She chooses a strong key and a proven symmetric cipher, encrypts her message, and sends the ciphertext to Bob.

2. Eve may intercept the message, but she must perform cryptanalysis to reveal its contents.

Symmetric cryptosystems are relatively simple and usually very fast for both encryption and decryption, but there is a significant challenge when using symmetric cryptography on a large scale: key distribution. Because Alice used a symmetric key algorithm to encrypt her message, she needs to also pass the key to Bob. She must not do this in a way that allows Eve to intercept the key, or all is lost. Alice and Bob could meet in person, but this becomes impractical if they are geographically remote from one another.

Alice could hire a trusted courier, but this is slow and doesn’t scale. If there are N people who must communicate securely, and you never share a single key with more than two people, the number of secret keys needed is:

MarcT0K (icons by JGraph), CC BY-SA 4.0 , via Wikimedia Commons

以下のようなユースケースで検討してください：

1. Alice ³ がBobに秘密メッセージを送信しようとしています。Aliceは強力な鍵と実績のある共通鍵暗号を選択し、彼女のメッセージを暗号化し、Bobに暗号文を送信します。

2. Eveはメッセージを傍受するかもしれませんが、Eveはその内容を明らかにするために暗号解析を実施しなくてはなりません。

共通鍵暗号システムは比較的単純で、暗号化と復号の両方で通常は非常に高速ですが、共通鍵暗号を大規模に利用する場合、非常に大きな課題があります：鍵の配布です。Aliceは彼女のメッセージを暗号化するために共通鍵アルゴリズムを用いたため、Bobに鍵も渡す必要があります。Aliceは、Eveが鍵を傍受できるような方法でこれをおこなってはいけません、そうでなければ全てを失います。AliceとBobは対面で会うこともできますが、地理的に遠隔な場合には現実的ではなくなります。

Aliceは信頼できる運び屋を雇うこともできますが、これは遅く、規模を大きくすることができません。もし安全に通信しなければならない人がN人いて、2人以上と単一の鍵を共有しない場合、必要となる秘密鍵の数は：

\(\frac{N \ast (N - 1)}{2}\)

Figure 2: For N = 1,000 people, you need to distribute, manage, and secure 499,500 keys

Despite the key distribution problem, we use symmetric ciphers extensively. They are computationally efficient and, in an order of magnitude, more efficient than the asymmetric ciphers we discuss below. You can encrypt large amounts of data in comparatively little time. The symmetric cipher’s advantage is speed.

鍵の配布問題はあるものの、共通鍵暗号は非常に使われています。共通鍵暗号は計算効率がよく、後述する非対称暗号よりも桁違いに効率が良いからです。比較的短時間で大量データを暗号化できます。共通鍵暗号の利点はスピードです。

Asymmetric Key Cryptography

Asymmetric Key Cryptosystems take a radically different approach to encryption and decryption, which greatly simplifies the problem of key distribution.

非対称鍵暗号方式

非対称鍵暗号方式は、暗号化と復号に対して根本的に異なるアプローチをとり、鍵の配布問題を大きく単純化します。

A Weak Analogy

Imagine Alice and Bob have a lockbox with the following properties:

1. The box has two distinct keys, one in Alice’s possession, the other in Bob’s possession,

2. When the box is locked with one of the keys, it can be unlocked only with the other, and vice versa.

As long as Alice and Bob keep their keys secure, this box has some useful properties:

1. Authentication: If Alice receives the box and it is locked, she knows it was Bob who locked the box,

2. Non-repudiation: Bob cannot deny having locked the box since it must have been locked with his key.

In this way, Alice and Bob can securely and confidently exchange physical objects without having to share a single lockbox key. Because Alice and Bob have their own personal keys that are not shared, they can have many different boxes that use the same key, and the counterparties can securely exchange objects without needing to create additional keys to exchange with additional parties.

弱い比喩

AliceとBobは以下のような性質の金庫を持っています：

1. 金庫は2つの異なる鍵があり、1つはAliceが持っており、もう1つはBobが持っています、

2. 金庫が鍵の1つで施錠されているとき、この金庫はもう一つの鍵でしか解錠できません。逆も同様です。

AliceとBobが鍵を安全に管理しているかぎり、この金庫はいくつかの有用な性質を持ちます：

1. 認証：Aliceが金庫を受け取り、それが施錠されている場合、AliceはBobがそれを施錠したとわかります、

2. 否認防止：Bobの鍵で施錠しなければならないため、Bobは金庫を施錠したことを否定できません。

この方法では、AliceとBobは安全に機密性を保って、単一の金庫の鍵を共有することなく、物理的なモノを交換できます。AliceとBobは共有しない個人の鍵を有しているため、同じ鍵を使う異なる金庫を大量に利用することができ、相手側は、追加の相手と交換するために追加の鍵を作成する必要なく、安全にオブジェクトを交換することができます。

New Directions in Cryptography

In 1976, Whitfield Diffie and Martin Helman released a paper, “New Directions in Cryptography” (Diffie 1976), based in part on previous work by Ralph Merkle . In the paper, Diffie and Helman describe techniques for securely exchanging secret keys and a technique for encrypting data using a pair of encryption keys. In 1977, Ron Rivest, Adi Shamir, and Leonard Adleman would go on to develop the first commercially viable asymmetric cryptosystem, RSA, based on the work of Diffie & Helman. ⁴

Asymmetric key cryptosystems are the foundation of cryptography on the Internet today. Every time you visit a secure HTTPS website, asymmetric key cryptography secures the connection.

The pair of keys in an asymmetric key cryptosystem are mathematically bound in a way that provides some very useful features. Analogous to the lockbox keys above, a message encrypted with one of the keys in the pair can only be decrypted with the other key. One of the keys is made public. The other is kept secret.

If Alice gives Bob her public key, Bob can use it to encrypt a message, and only the private key, kept secret by Alice, can decrypt the message. Likewise, if Bob has his own key pair and shares his public key with Alice, the two can now communicate securely without needing to pass a secret key back and forth. This solves the key distribution problem: For N people, you need only N key pairs.

暗号学の新しい次元

1976年、Whitfield Diffie氏とMartin Helman氏は、Ralph Merkle氏による過去の成果の一部をもとに、「New Directions in Cryptography」（Diffie 1976）という論文を発表しました。この論文では、Diffie氏とHelman氏は秘密鍵を安全に交換する手法および暗号鍵の一対の ペア を使ったデータの暗号化の手法について記述しています。1977年、Ron Rivest氏、Adi Shamir氏とLeonard Adleman氏は、Diffie氏とHelman氏の成果に基づいて、最初の商用利用可能な非対称暗号システムであるRSAの開発をおこないました。 ⁴

非対称鍵暗号システムは、今日のインターネットにおける暗号学の基礎です。安全なHTTPSのWebサイトに訪れるたびに、非対称鍵暗号が接続を安全にしています。

非対称鍵暗号システムにおける鍵のペアは、いくつか非常に有用な機能を提供する方法によって数学的にバインドされています。上述の金庫の鍵の比喩でたとえると、ペアの鍵の1つで暗号化されたメッセージはもう一方の鍵でしか復号できません。鍵の片方は公開されます。もう一方は秘密にします。

AliceがBobに自分の公開鍵を渡した場合、Bobはメッセージを暗号化し、Aliceが安全に管理している秘密鍵だけがそのメッセージを復号できます。同様に、Bobは自身の鍵ペアを持ち、公開鍵をAliceと共有している場合、2人は秘密鍵をやり取りすることなく安全に通信できます。これにより、鍵の配布の問題が解決されます：N人なら、必要な鍵ペアはN組だけです。

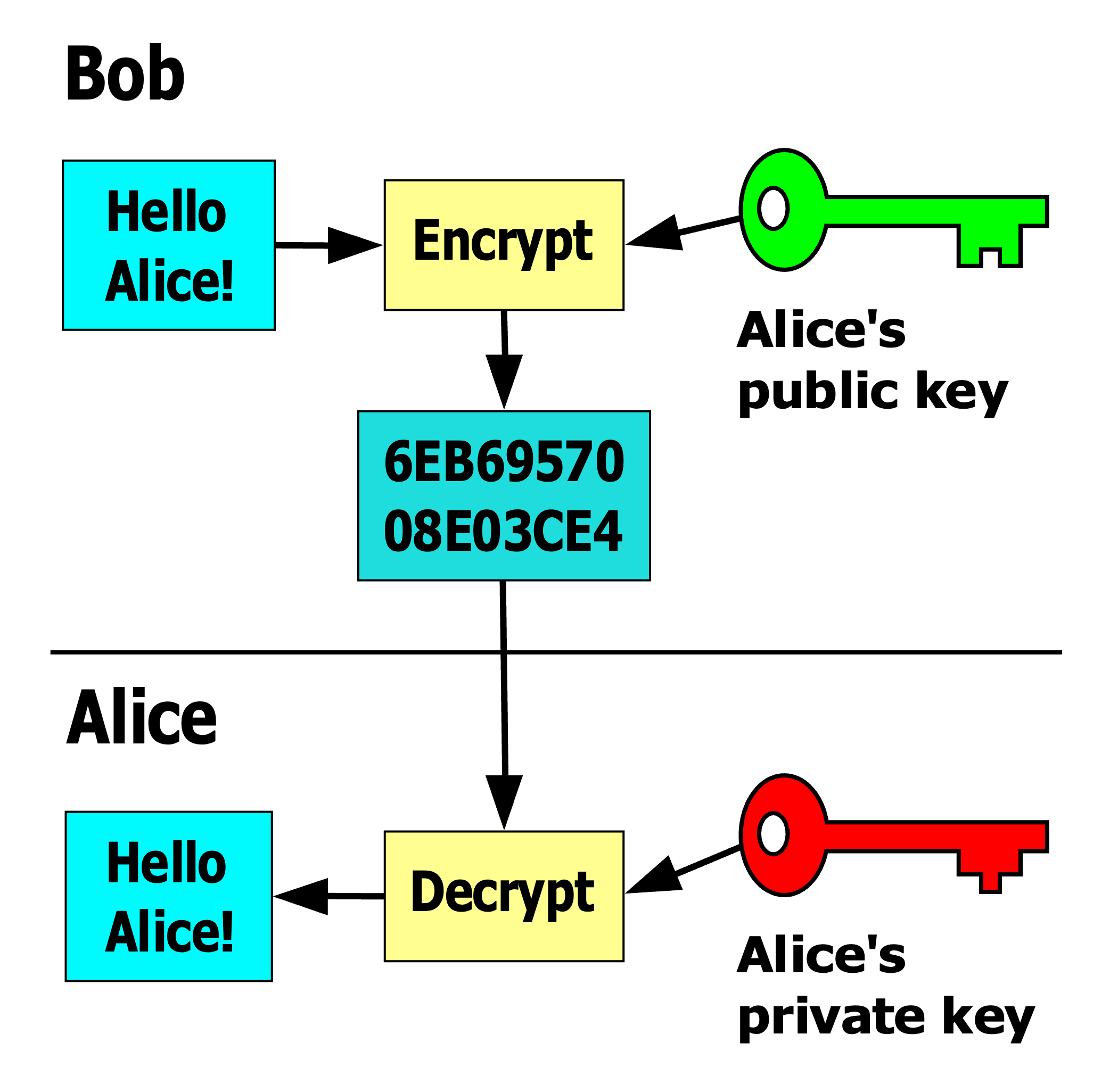
Figure 3: Asymmetric Key Cryptography

(Davidgothberg, Public domain, via Wikimedia Commons)

Another useful operation made possible with asymmetric key cryptography is message signing. Alice can use her private key to apply a digital signature to a message, and that signature can be verified with her public key. If Alice signs a message and sends it to Bob, Bob can confirm that the message did, in fact, come from Alice. This confirmation, if successful, also tells Bob the message was not tampered with after it was signed. Consider the following workflow:

1. Alice writes a message to Bob and signs it with her private key.

2. Alice encrypts the message with Bob’s public key and sends the message to Bob.

3. Bob decrypts the message with his private key.

4. Bob verifies the signature with Alice’s public key.

As a result, Alice has communicated securely with Bob, and Bob knows he can trust the message.

If this all seems too good to be true, fear not, there’s a downside! Public key encryption and signing are computationally much more expensive than symmetric key encryption, so much so that you would not want to regularly encrypt large amounts of data with asymmetric key encryption.

非対称鍵暗号で可能になるもう一つの有用な操作は、メッセージの署名です。Aliceは自分の秘密鍵を使ってメッセージに電子署名をすることができ、その署名はAliceの公開鍵で検証することができます。Aliceがメッセージに署名してBobに送信すると、Bobはそのメッセージが実際にAliceからのものだと確認できます。この確認が成功すれば、メッセージが署名された後に改竄されていないこともボブに伝えることができます。次のようなワークフローを追ってみましょう：

1. AliceはBobにメッセージを書き、彼女の秘密鍵によって署名します。

2. Aliceは、Bobの公開鍵によってメッセージを暗号化し、Bobにメッセージを送ります。

3. Bobは自分の秘密鍵でメッセージを復号します。

4. BobはAliceの公開鍵を使って署名を検証します。

結果として、AliceはBobと安全に通信することができ、Bobはメッセージを信頼できることがわかりました。

もし、これがすべて真実であるにはあまりに良すぎると思われたとしても、恐れることはありません、これにはデメリットもあります！公開鍵暗号化と署名は、共通鍵暗号化よりも計算量がはるかに多く、非対称鍵暗号化で大量のデータの暗号化を定期的にしたくないほどです。

The Best of Both Worlds

Modern cryptosystems combine both asymmetric and symmetric key cryptography to leverage the benefits of each. Asymmetric key cryptography is used to securely share a secret key, which is then used for the duration of the current transaction or session.

両方の世界のベスト

現代の暗号システムは、非対称鍵暗号システムと共通鍵暗号鍵システムの両方を組み合わせて、それぞれの利益を活用をします。非対称鍵暗号は安全に秘密鍵を共有するために用い、その秘密鍵は現在の取引やセッションの間だけ使います。

Conclusion

Understanding cryptography is fundamental to understanding information security, and central to information security is digital identity. While it is not necessary for most identity practitioners to understand the mathematics behind specific cryptographic techniques, understanding how cryptography works in general and how we use it is essential.

結論

暗号学を理解することは、情報セキュリティを理解するための基礎であり、情報セキュリティの中心はデジタルアイデンティティです。特定の暗号技術の背後にある数学を理解することはほとんどのアイデンティティ専門家にとっては不必要である一方、一般的に暗号がどのように動作し、我々がどのようにそれを使っているかを理解することは不可欠です。

Acknowledgments

The author thanks:

• Robert Sherwood and Matt Topper for their constructive feedback and contributions, and

• IDPro Principal Editor Heather Flanagan for all her assistance with the publishing process.

Going Further

There are many excellent resources for learning about cryptography and cryptanalysis. Some recommendations follow. See also the bibliography below.

Non-Technical Resources

• For an introduction to the history of cryptography, read Simon Singh’s “The Code Book” (Singh 2000).

• For a more comprehensive history of cryptography, read David Kahn’s “The Codebreakers” (Kahn 1996).

Technical Resources

• For a comprehensive technical dive into cryptography, consider Bruce Schneier’s “Applied Cryptography” (Schneier 2015).

• For an introduction to practical cryptanalysis, read Helen F. Gaines’ “Cryptanalysis: A Study of Ciphers and Their Solution” (Gaines 2014).

• If you have a penchant for coding, you’ll find extensive resources at Professor Bill Buchanan’s https://asecuritysite.com/ (Buchanan).

Author Bio

Mark Drummond

Mark Drummond is Director of Digital Trust and Identity at The Empire Life Insurance Company in Kingston, Ontario, Canada.

Bibliography

Buchanan, Bill. “Asecuritysite.Com.” Security and So Many Things. Accessed January 31, 2024. https://asecuritysite.com/.

Chapple, Mike, James Michael Stewart, and Darril Gibson. (ISC)2 CISSP Certified Information Systems Security Professional Official Study Guide. Ninth edition . Hoboken, NJ: John Wiley & Sons, Inc., 2021.

Diffie, W., and M. Hellman. “New Directions in Cryptography.” IEEE Transactions on Information Theory 22, no. 6 (1976): 644–654.

Gaines, Helen F. Cryptanalysis: A Study of Ciphers and Their Solution . Courier Corporation, 2014.

Garfinkel, Simson, and Gene Spafford. Practical UNIX and Internet security . O’Reilly Media, Inc., 1996.

Harris, Shon, and Fernando Maymí. CISSP All-in-One Exam Guide. Eighth edition . New York: McGraw-Hill, 2018.

Kahn, David. The Codebreakers: The Comprehensive History of Secret Communication from Ancient Times to the Internet . Simon and Schuster, 1996.

Kerckhoffs, Auguste. “La Cryptographie Militaire.” Journal des Sciences militaires , 9th series, IX (January 1883), 5-38 ; (February 1883), 161-191.

Menezes, Alfred J., Paul C. Van Oorschot, and Scott A. Vanstone. Handbook of Applied Cryptography . CRC Press, 2018.

Schneier, Bruce. Applied Cryptography : Protocols, Algorithms, and Source Code in C . 20th anniversary edition. Indianapolis, Indiana: Wiley, 2015.

Singh, Simon. The Code Book: The Science of Secrecy from Ancient Egypt to Quantum Cryptography . Anchor, 2000.

---